This free course is intended to provide a core of the mathematical skills that are used in college level science, technology, engineering, and mathematics (STEM) courses. It is not completed and will be completed as time permits.
In these days of standardized tests, geometry, algebra, and trigonometry are integrated. There are arguments for this pro-and-con. Formal proofs and derivations tend to be sacrificed for the sake of applied and integrated problems. That’s fine as long as the concepts and formulas aren’t thrown at a student, “here, use this,” without them knowing where it comes from. The course is a guide while learning in class (not a substitute for class) OR a quick review of the math we all need to brush up on from time to time. I have an agenda with it: to refer to these lectures, or even present them in class, when STEM students aren’t on board with what’s assumed in a college course.
About half of the lectures are completed with about half of the video time consumed: free courses must remain under 2 hours.
Here are the lecture descriptions:
Parallel Lines Cut by a Transect [completed]
We start with some elementary definitions of lines, rays, and angles, and then learn the equivalences of the angles around two parallel lines cut by another line. This leads to a proof: the sum of the interior angles of a triangle sum to 180 degrees. These relationships and the proof set the stage for studying the properties of other geometric figures, and are applied in many drawings to describe and solve problems in science, technology, engineering, and mathematics (STEM). If I had a dollar for every time this arrangement is used in a STEM proof, I would be a trillionaire (move over Bezos).
Some Properties and Formulas for Triangles [pending]
In this presentation [when available] we look at triangles. In the preceding lecture we’ve already proved the most important formula for triangles: the sum of their interior angles is 180 degrees. After defining the four main types of triangles, we’ll then prove the formula for the area of a triangle. The four types of triangles are:
Scalene: this is your random triangle folks, the one that does not have any particular defining relationship between its sides and angles.
Isosceles: this is a triangle with two equal sides, the third may or may not be equal. When this case occurs, it turns out the two base angles are also equal.
Equilateral: this is a triangle with all three sides equal, thus it is a type of isosceles triangle with two sides equal (and also the third). In this case, all of the interior angles are 60 degrees.
Right triangle: this is a triangle where one of the angles is 90 degrees. The two legs forming the 90 degree angle are called legs, and last side connecting the legs called the hypotenuse. Certainly the right triangle is important because it can be used in corners, but more importantly, it forms the core of trigonometry, used in the definition of the three main trigonometric functions: sine, cosine, and tangent.
The Equation of a Line [pending, but exercise available]
Before we cover quadrilaterals in the next lecture, we review the equation of a line. There are many different types of quadrilaterals, and their classification depends upon congruence of various angles, sides, and diagonals on these figures. In addition to being given diagrams of each with their defining properties, the various figures are plotted in the Cartesian space (standard graph paper) and these angles, sides, and diagonals are proven using the slopes of lines.
The lectures on lines and quadrilaterals are not ready at this point. However a review exercise for lines is provided in “external resources.” Use the exercise to test your understanding of lines. If you are confident in plotting points, you do not need equation for a line or quadrilaterals to review the lectures on transformations.
Quadrilaterals [pending]
There are many different types of quadrilaterals, and their classification depends upon congruence of their various angles, sides, and diagonals when reviewing their diagrams. In addition to being given diagrams of each, and their classification according to each of their defining properties, the various figures are plotted in the Cartesian space (standard graph paper). The defining relationships of the angles, sides, and diagonals are proven for each.
Understanding the preceding lecture on lines will increase the understanding of this presentation. However, if you are confident enough in plotting points according to their ordered pairs, you do NOT need the equation for a line or quadrilaterals to review the next lectures on transformations.
Transformations [completed: 4 Lectures]
Transformations are mathematical operations that “transform” (change) a figure (2D) or object (3D) in the “space” in which it is plotted. These transformations can be “isometric,” preserving the distances and angles of the figure or object, or “non-isometric,” where the figure or object can be scaled (changed in size) or deformed (changed in shape such as skewed). We will cover the most common isometric examples 1) translation: moving a figure or object in “space,” 2) rotation, rotating a figure about a point, and 3) reflection, where the figure or object is reflected by a line or plane. We then look at “composites,” combinations of transformations that are performed sequentially, with the result depending upon the sequential order of the transformations.
We restrict this discussion to two-dimensional (2D) figures.
We look at the “rules” of each operation and what they do to the ordered pairs (x,y) of the points that define the figure.
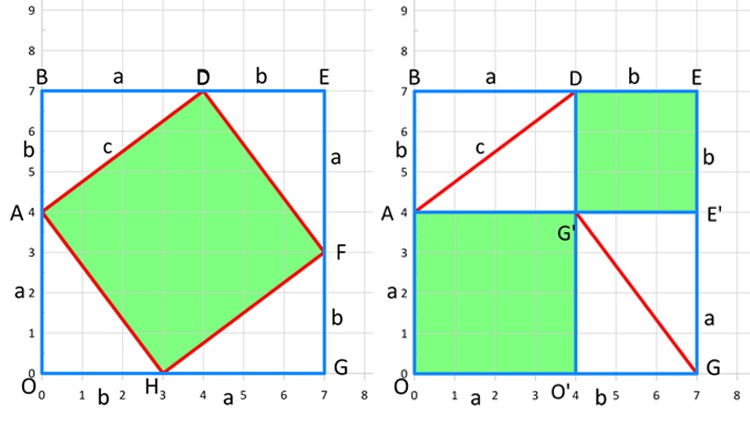
An Interesting Proof [exercises and their answers complete the proof; a video following the exercises/ proof is pending].
We prove the Pythagorean theorem using translations from the previous section on transformations! The proof is centered on two quadrilaterals, but they are the easy one everyone knows: the square. We’ll prove the two figures are squares first, but it is straightforward from inspection. The Pythagorean theorem, restated as “the distance formula,” is used to calculate distances given sides of right triangles. It is thus usually used in math classes long before it is proven. The Pythagorean theorem is also used to define a circle. In the next lecture, we then look at the circle that forms the core of trigonometry, the “unit” (radius = 1) circle.
Though the presentation is not yet available, two “Google Forms” present the proof as an exercise. The presentation will follow this proof.
The Unit Circle: the Core of Trigonometry [pending]
In this presentation, we use the Pythagorean theorem along with the definition of sine and cosine to describe a “unit” (radius = 1) circle. We plot the points of some special commonly used angles.
An Equation for a Wave [pending]
Let the unit circle roll!!!!!!!! We let the unit circle roll while plotting sine (or cosine) and we get a wave. HOW COOL IS THAT???. We look at the resultant formula that defines that wave, then tweak it a bit.
Triangulation [pending]
We use the law of sines to calculate the distance to a mountain when we know a baseline between two points sighting on the mountain. We then calculate its height using the tangent function and an angle measured between the summit and the horizontal.
